1. GPS Signal Characteristics
1.1. Signal structure
GPS satellite transmits signals at two frequencies, designated L1 and L2 on which three binary modulations are impressed. The C/A- code, the P(Y) code and broadcast (or navigation) message. L1 is the principal GPS carrier signal with a frequency of 1575.45 MHz and is modulated with the P(Y) code, C/A code and navigation message. The second signal L2 is transmitted at a frequency of 1227.60 MHz and is modulated with only P(Y) code and navigation message. The second signal was primarily established to provide a means of estimating the ionospheric delay to GPS measurements (Each GPs satellite also transmits a L3 signal at 1381.05 MHz associated with its dual role as a nuclear blast detection satellite, as well as S band telemetry signal, however these will not be discussed further).
The `Precision’ P(Y) –code has a bit rate of 10.23 MHz while `Coarse/Acquisition’ C/A code and navigation message have bit rate of 1.023 MHz and 50 Hz respectively. The P(Y) code is an encryption of published P-code by a code sequence referred to as W-code (resulting in the so called `Y code’) and accessible only by US Department of Defence (and other authorized user). The encryption of P-code was imposed on 31 January 1994 for all satellites under so called Anti- Spoofing Policy.
All the signals transmitted by GPS satellites are right hand polarized, coherently derived from a basic frequency of 10.23 MHz and are transmitted within a band width of above 20-46 MHz by a shaped-beam antenna array on the nadir-facing side of the satellite. Each satellite transmit a unique C/A code and a unique 1 week long segment of P(Y) code signals on L1 and L2 respectively, and 28.8 dbw for C/A code signal dbw indicates actual power of a signal compared to reference of 1 watt. The strength of the electromagnetic wave decreases during propagation primarily as a function of transmitter – receiver distance. Thus, the GPS signal arriving at the receiver antenna is relatively weak, with roughly the same strength as the signal from the geo-stationary TV satellites. However, the carefully designed GPS signal structure allows the use of small antennas, as opposed to large TV dishes.
Since both the signal transmitting satellite and the receiver move with respect to each other, the signal arriving at the antenna rotating with earth is Doppler shifted. Consequently the received frequency differs from transmitted frequency by an amount which is proportional to the radial velocity of the satellite with respect to the receiver. Signals from different satellites therefore arrive at the received antenna with different Doppler-shifted frequencies.
1.2. Signal Coverage
The GPS signal is transmitted by the satellite towards the earth in the form of a single beam. In order to achieve high accuracy, positioning by GPS has to be performed in the differential mode. In this mode, two GPS receivers observe the same satellite, at the same time, and the relative position between two receivers is estimated. If one considers the spatial coverage of the GPS signal from a satellite then distances between two points on the earth’s surface that can still view the same satellite, as a function of the observation mask angle. With an elevation mask angle of 150, two receivers on earth’s surface separated as far apart as 13,500 km can still view the same GPS satellite. However, both receivers `see’ the signal very near the horizon and in general, since the signal will be obstructed by either topography or objects around the antenna, receiver separators will be much less than those shown in following figure. For most surveying/ mapping applications, maximum receiver separations are of the order of tens of kilometers.
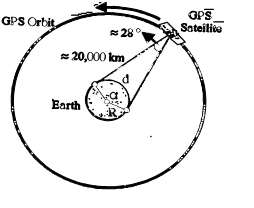
Figure 1: GPS Signal Coverage
| Mask Angle | a | Arc length (d) |
| 0°5°10°15° | 152°142°132°122° | 16889 km15778 km14667 km13556 km |
|
Earth Radius R » 6378 km Mask Angle= Minimum elevation of observed satellite |
||
Table 1: GPS Signal Coverage with Mask Angle
1.1. Codes and Pseudo range measurements
1.1.1. Pseudo-random noise codes
There are two Pseudo-Random Noise (PRN) codes which are modulated on the signals transmitted by GPS satellites.
- The P(Y) code and
- The C/A code.
The two main functions of these codes are
- To provide time delay measurements so the user can determine the distance from receiver’s antenna to observed satellite (either code could be used, but the P(Y) code provides a more precise range estimate than the C/A code)
- To help the receiver in differentiating the incoming signals from different satellites. These codes are sequences of binary values (zeros and ones), and although the sequence appears to be random, each code has unique structure generated by mathematical algorithm one version of the code is generated within the satellite, and identical code sequence is replicated within the receiver. Two such identical codes will only be aligned at zero lag (i.e. when the sequence of one code is time shifted to the instant when all the Os and 1s in that code match the sequence in the other code). Because the codes are generated by either the satellite clock, or receiver clock, they are in-fact a means of representing the time defined by the respective clock. If two clocks are synchronized to the same time system, then clock times can be compared and the difference is a measure of time taken for a signal to travel from satellite to receiver. From this the distance can be estimated.
Each C/A code is unique sequence of 1023 binary numbers which repeats itself in 1ms. Each binary bit of C/A code is generated, at the rate of 1.023 MHZ and has a ‘duration’ or ‘length’ of approximately 1 μs (or about 293m in units of length).
In contrast to the C/A code, the P(Y) code consists much longer binary sequence of 2.3547 x 1014 binary numbers, and its pattern will not repeat itself until after 266 days. The P(Y) code is generated at a rate ten times faster than the C/A code i.e. 10.23 MHz. This means each bit has duration of approximately 0.1 μs (or a ‘length’ of above 29m). Each GPS satellite is assigned a unique 1 week’s segment of the P(Y) code and the segment is set back to zero each week at midnight (OhUT) from Saturday to Sunday.
1.1.2. Determining Satellite – receiver range
By acquiring C/A code or P(Y) code, the observer can measure the distance or range to the satellite. The basic principle for obtaining range is the so-called ‘code correlation’ technique whereby the incoming code from the satellite is correlated with a replica of the corresponding code generated inside the receiver, as depicted in the figure 2 (A) and(B) .
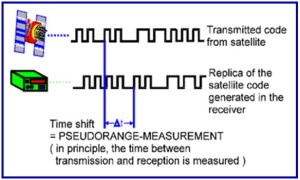
Figure 2: (A)
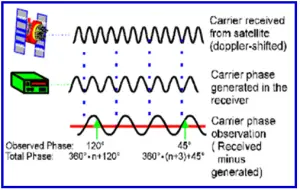
Figure 2: (B)
Figure 2: (A) and (B) showing PseudoRange and Carrier Phase Measurement
Both codes are generated using the same mathematical algorithm. The time shift (dt) required to align the two codes is, in principle, the time required by the signal carrying the code to travel from the satellite to the receiver. Multiplying dt with speed of light results in an estimate of range. This range is referred to as a pseudo range, because it is still biased by the time offset (or mis-synchronization) between satellite clock and the receiver clock and used to measure the time delay.
In general, the precision of a pseudo range measurement is about 1 percent of its code length (or resolution). The nominal precision of the P(Y) code pseudo range is therefore, 0.3m and for C/A code pseudo range it is above 3 m. Besides being more precise, the P(Y) code pseudo range measurement is more resistant to the effects of multi-path and jamming/interference. Moreover, since P(Y) code is modulated on both the L1 and L2 signals, the user can obtain pseudo range measurement at both the frequencies, i.e. the P(Y)-L1 pseudo range and P(Y)-L2 pseudo range, so that by combining those two measurements it is possible to derive a new pseudo range that is not affected by ionospheric delay. However due to Anti Spoofing (AS) policy only authorized user can gain access to the P(Y) code directly to make pseudo range measurement using code correlation technique. Civilian users have to employ different signal processing technique to make dual frequency measurements. Apart from receivers used for many GPS surveying applications, where dual frequency measurements are a pre-requisite for obtaining fast centimetre level accuracy coordinates, most civilian GPS receiver intended for navigation applications only observe C/A code pseudo range, and hence are referred to as single frequency navigation receivers.
1.2. Broadcast navigation message
Besides the ranging codes, GPS signals are also modulated with the navigation message. This contains information such as the satellites orbital data (the so-called broadcast ephemeris) Satellite almanac data, satellite clock correction parameters, satellite health and constellation status, ionospheric model parameters for single frequency users, and the offset between GPS and UTC (Universal Time Coordinated) time system. The content of the navigation message is continuously updated by GPS control segment and broadcast to the user by GPS Satellites.
1.3. Ephemeris
An ephemeris is a list of coordinates defining the orbital position of a satellite at various times. All GPS measurement processing techniques require the input of ephemeredes for the time span of the observations in order to determine ground receiver position, either absolute in point positioning mode or relative when deployed in a differential mode. Ephemeredes can be generally classed either as post processed or predicted.
1.3.1. The post –processed ephemeris (Precise)
The post –processed ephemeris (Precise) are determined after observations are made to the satellite and is therefore an estimate of the satellite’s position in the period of observations. Tracking data are acquired from a number of fixed stations and processed in order to obtain the orbit that best fits the data in a least square sense.
1.3.2. The Broadcast Ephemeris
The Broadcast Ephemeriswhich are obtained by extrapolating a post- processed orbit for a few days into the future, allow real time positioning using pseudo-ranges.
These broadcast ephemeris are generated in two steps –
- Based on seven days of observations from five Monitor Stations, is generated using highly sophisticated software package for orbit determination.
- In the second step (on-line) the discrepancies between the current observation at the Monitor Stations and the reference ephemeris are derived and corrections to be applied to the reference ephemeris. Satellite positions estimated in the above process are then represented in the form of Keplarian elements with additional perturbation parameters. Hence the representation of satellite trajectory is achieved.
1.4. Carrier Waves and Carrier Phase Measurements
The main function of GPS carrier waves L1 and L2 is to carry ‘PRN’ codes and navigation message to the receiver. The codes and navigation messages are modulated as carrier waves using bi-phase shift key modulation technique as shown in the following figure 3.
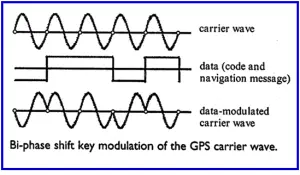
Figure 3: Bi-phase Shift Key Modulation of the GPS Carrier Wave
When the data (code and navigation message) value for a binary bit 0 and it changes to value of 1 (or vice versa 1 to 0) then the carrier phase is shifted by 180°. When there is no change in the value of adjacent bits then there is no change in the phase.
Phase measurements made on the carrier waves can also be used to derive very precise range measurements to the satellites, which are sometimes, referred to also as ‘ Phase Ranges’ or ‘Carrier Ranges’ or simply carrier measurements. For precise GPS applications such as for surveying and geodesy, carrier phase measurements must be used in place of pseudo ranges.
1.5. Ambiguous Carrier Phase
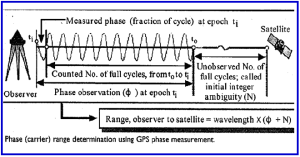
The carrier phase measurement is the difference between the reference phase signal (which has the form of sine wave) generated by the receiver and phase of incoming GPS signal (after stripping away the code and navigation message modulations) and is in fact a beat signal. The measurement of phase by a GPS receiver is complicated by the fact that the receiver can not measure directly the complete range from receiver to the satellite. At the initial epoch of signal acquisition (to) only the fraction of cycle of beat phase can be measured by the receiver. (One cycle corresponds to one wavelength of sine wave that is carrier signal without modulation, which for the L1 carrier wave is 19 cm and L2 is approximately 24 cm). The remaining integer number of cycles to the satellite can not be measured directly. The unknown integer number of cycles is usually termed as ‘initial cycle (phase) ambiguity (N)’. Subsequently, the receiver only counts the number of integer cycles that are being tracked. As long as there is no loss – of – lock of tracking of the satellite in value of N remains a constant.
The phase measurement at a certain epoch ti i.e. f (ti), is therefore equal to the fractional phase (Fr) at that epoch augmented with number of full cycles ‘counted’ (Int) since to
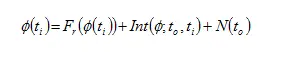
The above equation indicates that the GPS carrier phase measurement (when expressed in length units) is not true or absolute range from receiver to the satellite, as in the case of pseudo range, but is an ambiguous range. There is an unobserved part of the range caused by initial cycle ambiguity of the phase as illustrated in the following figure. In order to convert this ambiguous range into a true range, the cycle ambiguity N has to be estimated. If the value of the cycle ambiguity can be correctly estimated, then the resultant carrier range will be transformed into a very precise range measurement and can be used for high precision positioning. However, the carrier range has the opposite ionospheric effect to the regular pseudo range. Correctly estimating value of the integer cycle ambiguity is not an easy task. This computation is referred to as ambiguity resolution.
Figure 4: Carrier Phase – Range Measurement
1.6. GPS Signal Propagation
In its propagation from the satellite to the observer’s antenna the signal has to travel through several layers of the atmosphere. Due to the refraction inside the ionosphere and ionospheric layers, the speed and direction of signal will be affected and in turn the measured pseudo ranges and carrier phase will be biased. In addition, signal propagation may be influenced by other phenomenon such as intentional or accidental interference due to multipath and jamming.
1.6.1. Ionospheric and Tropospheric Delay
The ionosphere will affect the speed, frequency, direction and polarization of GPS signals, as well as cause amplitude and phase scintillation. By far the largest effect will be on speed of the signals, which will directly affect the carrier range and pseudo range measurements to the satellite. The ionosphere will delay the code measurement (the pseudo range) and advance the signal phase (the carrier range), by the same amount.
The slant range error caused by the ionosphere can be up to about 100m, and its magnitude is dependent on factors such as the time of the day (the ionosphere is quieter at night), latitude of the observer, time of the year, period within the 11 year sunspot cycle (the highest ionospheric activity for the current cycle was in 2001), elevation angle to the satellite, and frequency of the signal. The estimated maximum rate of change of ionospheric propagation delay is about 19 cm/s, which correspond to about 1 cycle on L1. Very rapidly changing ionospheric condition can cause losses of lock, especially on L2 frequency under AS. When dual frequency observations are available, a linear combination of measurements made on L1 and L2 can be constructed that eliminates the first order ionospheric delay.
The troposphere will also affect the speed and direction of GPS signals, as well as cause some attenuation of the signal. As with the ionosphere, the largest effect will be on speed of signal and, in this case, the troposphere will delay both the code and phase measurements by the same amount. The tropospheric delay effects are of the order of 2 – 25m, a minimum in the vertical direction and becoming larger as the elevation angle of the signal reduces down to the horizon. Both wet and dry components of the troposphere contribute to the delay, with the former being most difficult to estimate. The troposphere is only 10 km thick, hence signal reaching high altitude points will have less troposphere to travel through, and hence will experience less tropospheric delay.
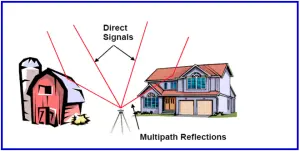
1.6.2. Multipath Effects
In addition, the GPS signal can experience multipath, a phenomenon in which a signal arrive at antenna via two or more paths, that is a direct signal and one or more reflected signals. The signals will interfere with each other and the resultant signal will cause error in pseudo range and carrier phase measurement. The range errors caused by multipath will vary depending on relative geometry of the satellites, reflecting surface and GPS antenna; and also the properties and dynamics of the reflecting surface. In case of carrier phase, multipath effect can be up to 5 cm, i.e. 0.25 cycles of wave length; while for pseudo ranges it can be many tens of meters.
Figure 5: Multipath Reflections
Multipath is considered one of the limiting factors to improvements in GPS carrier phase based positioning ‘productivity’. That is, the presence of multipath disturbance impacts on the reliability of ambiguity resolution, particularly when observation sessions are very short. Hence strategies must be implemented that deal with such eventualities, such as making extra (redundant) surveys of the same point. It should also be noted here that in order to be used for positioning the signal transmitted by the satellites has to reach the GPS antenna. If the satellite signal is blocked by Topography, foliage or other structures than measurements can not be made. GPs positioning therefore can not be performed in tunnels, in door or under water. In areas with many high rising buildings and tall trees that can obstruct the signal reception from satellite, it can also be expected that positioning with GPS will be less optimal technique than in relative open areas. There are a few strategies that can be used to overcome the signal obstruction problem. The obvious one is to choose a location for the antenna site that has the clearest visibility to the sky citing of antennas near sources of microwave radiation is to be avoided wherever possible so as to minimise the chances of accidental jamming of the GPS signal.
Read related article:
- Introduction to GPS
- GPS Surveying Techniques
- GPS Field Observation and Data Processing
- Possible Applications of GPS
I wonder these two statements regarding the code and phase velocities:
-The ionosphere will delay the code measurement (the pseudo range) and advance the signal phase (the carrier range), by the same amount.
-the troposphere will delay both the code and phase measurements by the same amount.