The principle underlying spatial interpolation is the First Law of Geography. Formulated by Waldo Tobler, this law states that everything is related to everything else, but near things are more related than distant things.
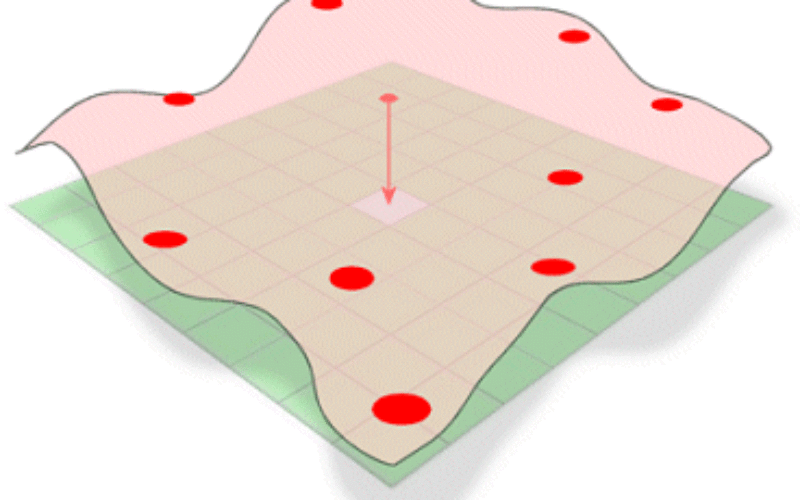
Spatial interpolation is the process of using points with known values to estimate values at other unknown points. For example, to make a precipitation (rainfall) map for your country, you will not find enough evenly spread weather stations to cover the entire region. Spatial interpolation can estimate the temperatures at locations without recorded data by using known temperature readings at nearby weather stations. This type of interpolated surface is often called a statistical surface. Elevation data, precipitation, snow accumulation, water table and population density are other types of data that can be computed using interpolation.
Choosing a correct type of interpolation method depends on many factors. There is no general method that is suitable for all problems: it depends on the nature of the variable and on the time-scale on which the variable is represented.

Courtesy @ ESRI
There are different methods of interpolation. Choosing an interpolation method is influenced by knowledge of the surface for modeling. Each method works differently, but most utilize the concept of spatial auto-correlation; near things are more alike than things far away.
Rather than assume one interpolation method is better than another, we should try different interpolation methods and compare the results to determine the best interpolation method for a given project.
- The quality of sample point set can affect choice of interpolation method as well. If the sample points are poorly distributed or there are few of them, the surface might not represent the actual terrain very well. If we have too few sample points, add more sample points in areas where the terrain changes abruptly or frequently, then try using Kriging.
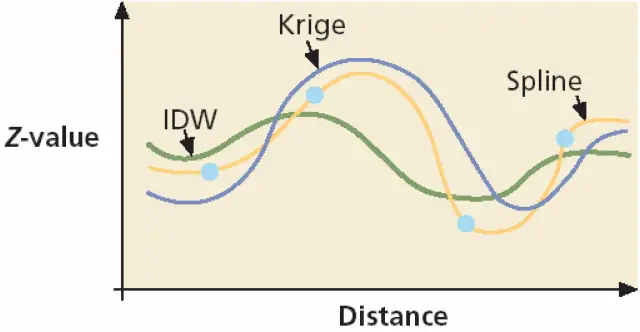
- The real-world knowledge of the subject matter will initially affect which interpolation method to use. If it is know that some of the features in surface exceed the z value, for example, and that IDW will result in a surface that does not exceed the highest or lowest z value in the sample point set, choose the Spline method.
- If we know that the splined surface might end up with features that we know don’t exist because Spline interpolation doesn’t work well with sample points that are close together and have extreme differences in value, you might decide to try IDW.
When we measure elevation, the depth of a well, or the level of noise, we make that measurement at a precise location. A point layer can represent a set of measurements. The location of the points and the point values form the basis for interpolation. The most used and promising techniques are universal Kriging and linear regression models in combination with Kriging (residual Kriging) or IDW.
E.g.:
- Air temperature data – Kriging is most likely to produce the best estimation of a continuous surface, followed by IDW and then Spline.
- Mining: Kriging.
- IDW interprets spatial autocorrelation in a literal fashion. A surface created with IDW will not exceed the known value range or pass through any of the sample points. IDW is a good interpolator for phenomena whose distribution is strongly correlated with distance, such as noise. In some cases, the accuracy of an IDW surface can be improved by using line layers as barriers.
- The Splineinterpolation method incorporates a curvilinear model as part of the calculation. A surface created with Splinecan exceed the known value range, but must pass through all of the sample points.
- Krigingis one of the most complex interpolators. It measures the relationships between all of the sample points and then predicts the cell value. A surface created with Krigingcan exceed the known value range, but does not pass through any of the sample points.
- Global Kriging (GK) is the best ranked method for all climate variables except maximum temperature.
References:
- Comparison of six methods for the interpolation of daily,European climate data by Nynke Hofstra, et. all; Journal of Geophysical Research, Vol. 113, D21110, doi:10.1029/2008JD010100, 2008.
- Interpolation methods for climate data literature review by R. Sluiter.
- Spatial Interpolation of Rainfall Data Using ArcGIS: A aComparative Study by Julie Earls et. all.
Related Topics: